Ohm’s Law in Real Life: How Voltage, Current, and Resistance Shape Everyday Technology

Ohm’s Law is more than a formula engineers memorize—it’s a practical rule that quietly governs how nearly every electronic device behaves. From preventing LEDs from burning out to estimating the power your gadgets consume, Ohm’s Law explains the everyday relationship between voltage, current, and resistance in simple, real-world terms.

Table of Contents

  1. Introduction: Why Ohm’s Law Matters Beyond the Classroom
  2. The Core Idea: Voltage, Current, Resistance
  3. Real-Life Example #1: Limiting LED Current
  4. Real-Life Example #2: Calculating Power Consumption at Home
  5. Why Ohm’s Law Still Matters in Modern Electronics
  6. Top 5 Frequently Asked Questions
  7. Final Thoughts
  8. Resources

Introduction: Why Ohm’s Law Matters Beyond the Classroom

Ohm’s Law—stated simply as V = I × R—is often introduced as a math exercise. But in the real world, it’s a decision-making tool used by engineers, electricians, product designers, and hobbyists.
Whenever you want to know:

  • Why a phone charger heats up
  • Why LEDs need resistors
  • How much power a device actually consumes
  • Why a device stops working after a cable gets damaged
  • Why long extension cords reduce performance

…you’re relying on the logic behind Ohm’s Law.
Its power is not in the equation itself but in its ability to explain cause and effect in electrical systems.

The Core Idea: Voltage, Current, Resistance

Ohm’s Law links three quantities you encounter every time you use an electronic device.

Voltage as the “Push”

Voltage is electrical pressure.
It is the force that pushes electrons through a conductor.
Real-life analogy:
Water pressure in a pipe. Higher pressure = more force pushing water forward.

Current as the “Flow”

Current is the movement of electrical charge.
Analogy:
The amount of water flowing per second.

Resistance as the “Control”

Resistance restricts current.
Every material has resistance—even copper wires.
Analogy:
A narrower pipe that limits water flow.
Together, these three define how electricity behaves. When you change one, the others react.

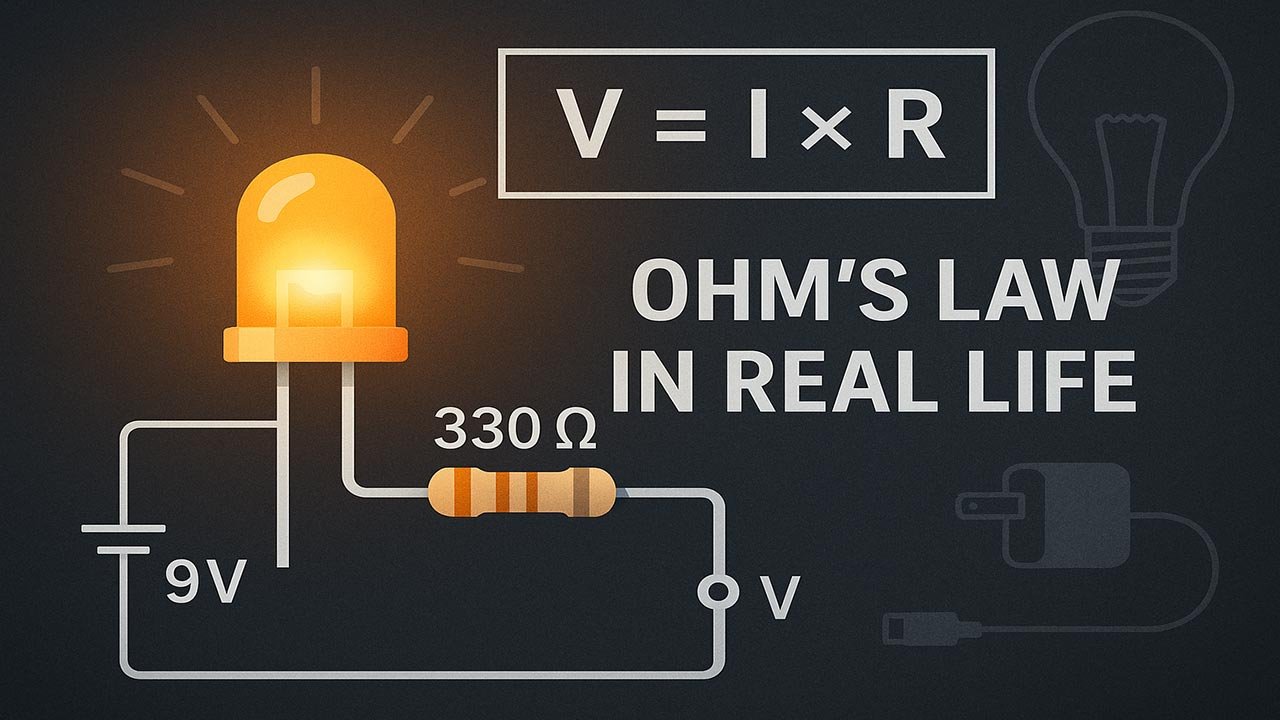
Real-Life Example #1: Limiting LED Current

LEDs are incredibly efficient—but also incredibly fragile. They don’t limit their own current. That means if you connect an LED directly to a battery, it often burns out instantly.

Why LEDs Burn Out Without a Resistor

Most LEDs require 20 mA or less to operate safely.
But a 9V battery can deliver far more without resistance.
An LED typically has:

  • A forward voltage of about 2V (depends on color)
  • A safe operating current of 20mA (0.02A)

When connected directly to a 9V battery, the remaining voltage “excess” forces far more current than the LED can tolerate.
Ohm’s Law explains why this is dangerous:

Current = Voltage / Resistance

No resistor → almost no resistance → extremely high current → destroyed LED.

How to Calculate the Right Resistor

To protect the LED, we add a resistor to limit current.
Step 1: Determine voltage across the resistor
9V (battery) − 2V (LED) = 7V
Step 2: Decide target current
I = 20mA = 0.02A
Step 3: Use Ohm’s Law
R = V ÷ I
R = 7V ÷ 0.02A = 350Ω
Use a 330Ω or 360Ω resistor.
Either value will be safe.
This is why nearly every LED circuit includes a resistor: Ohm’s Law ensures current stays within safe limits.
What happens if you increase the resistor?
Current drops → LED gets dimmer.
What happens if you decrease the resistor?
Current rises → brightness increases → LED may burn out.
This example shows Ohm’s Law as a practical design tool, not a math quiz.

Real-Life Example #2: Calculating Power Consumption at Home

Your monthly electric bill is based on energy used—measured in kilowatt-hours (kWh).
But power (W) comes directly from Ohm’s Law.

How Ohm’s Law Helps Explain Power Bills

Power is calculated with:

P = V × I

If you know the voltage of your system and how much current a device draws, you can instantly calculate power consumption.
Most homes in North America use 120V outlets.
Europe uses 230V.

Practical Power Calculations

Example: A 60W lightbulb

A classic incandescent bulb might draw:

I = P / V
I = 60W / 120V = 0.5A

So that 60W bulb pulls half an amp.

Example: A phone charger

Most chargers use about 10W.

I = 10W / 120V = 0.083A

This explains why chargers feel warm—they’re handling current and converting energy into heat.

Example: A space heater

A 1500W heater:

I = 1500W / 120V = 12.5A

This is why heaters frequently trip breakers: they consume a large share of your circuit’s safe capacity (usually 15A).

Example: Why thin extension cords get hot

If a cord has higher resistance, and a high-power device draws high current, the cord itself dissipates power:

P = I² × R

Even slight resistance increases become dangerous under heavy loads.
This is why extension cords are labeled with amp ratings—and why Ohm’s Law helps prevent fires.

Why Ohm’s Law Still Matters in Modern Electronics

Even in advanced circuits using microcontrollers, switching power supplies, and semiconductor devices, Ohm’s Law remains the underlying rule that determines:

  • component sizing
  • safe current levels
  • thermal behavior
  • wire gauge selection
  • LED behavior
  • battery life estimation
  • voltage drop calculations

Modern engineering still depends on these fundamentals.
Ohm’s Law persists because electricity itself obeys it. Even the most complex devices are built from components that follow these simple relationships.

Top 5 Frequently Asked Questions

Incandescent bulbs naturally limit their own current because their filament increases resistance as it heats up. LEDs do not—they will draw as much current as available unless externally restricted.
The voltage is fixed (5V), but the current rating is the maximum the charger can safely supply. Devices only draw the current they need.
Current increases in proportion to the voltage. This can overheat components, burn out LEDs, damage circuits, or cause fires.
Wires have resistance. Over long distances, that resistance becomes significant, reducing the voltage available at the end.
By ensuring current stays within safe limits for wires and components. Exceeding current ratings generates heat, which can melt insulation or ignite materials.

Final Thoughts

The most important takeaway is this: Ohm’s Law is a predictive tool.
It tells you what will happen when electrical conditions change.

  • Increase voltage → current rises
  • Increase resistance → current falls
  • Decrease resistance → components heat up
  • Increase current → power consumption increases

From protecting a single LED to preventing an overloaded home circuit, Ohm’s Law empowers you to make safe, informed decisions about electricity. It explains failure modes, guides design choices, and forms the core of electrical troubleshooting.
Once you internalize the push-flow-control relationship between voltage, current, and resistance, electronics stop feeling mysterious—and start becoming intuitive.